1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
| #include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
#include <vector>
#include <map>
#include <set>
#define MAXN 105
#define INF 0x3f3f3f3f
#define p 998244353
#define rint register int
#define LL long long
#define LD long double
using namespace std;
int n, m, x, y, a[MAXN][MAXN], c[MAXN][MAXN], ans[MAXN][MAXN];
map<int, int> mp;
void mul(int a[MAXN][MAXN], int b[MAXN][MAXN])
{
for(rint i=1; i<=n; ++i)
for(rint j=1; j<=n; ++j)
{
c[i][j]=0;
for(rint k=1; k<=n; ++k) c[i][j]=(c[i][j]+1LL*a[i][k]*b[k][j])%(p-1);
}
memcpy(a, c, sizeof(c));
}
void ksm1(int a[MAXN][MAXN], int y)
{
for(rint i=1; i<=n; ++i) ans[i][i]=1;
while(y)
{
if(y&1) mul(ans, a);
mul(a, a); y>>=1;
}
}
int ksm(int x, int y)
{
int ans=1;
while(y)
{
if(y&1) ans=1LL*ans*x%p;
y>>=1; x=1LL*x*x%p;
}
return ans;
}
int bsgs(int a, int b)
{
int siz=sqrt(p)+0.5, base=1;
int t=b;
mp[t]=0;
for(rint i=1; i<=siz; ++i)
{
t=1LL*t*a%p;
mp[t]=i;
base=1LL*base*a%p;
}
t=1;
for(rint i=1; i<=siz; ++i)
{
t=1LL*t*base%p;
if(mp.count(t))
{
int x=i*siz-mp[t];
return x;
}
}
return -1;
}
int exgcd(int a, int b, LL& x, LL& y)
{
if(!b)
{
x=1, y=0;
return a;
}
int d=exgcd(b, a%b, x, y);
int temp=x; x=y, y=temp-a/b*y;
return d;
}
int solve(int a, int b, int c)
{
LL x, y;
int d=exgcd(a, b, x, y);
if(c%d) return -1;
x*=c/d;
return (x%(b/d)+(b/d))%(b/d);
}
int main()
{
scanf("%d", &n);
for(rint i=1; i<=n; ++i) scanf("%d", &a[1][i]);
for(rint i=2; i<=n; ++i) a[i][i-1]=1;
scanf("%d%d", &m, &y);
ksm1(a, m-n);
x=solve(ans[1][1], p-1, bsgs(3, y));
if(x==-1) printf("-1\n");
else printf("%d\n", ksm(3, x));
return 0;
}
|
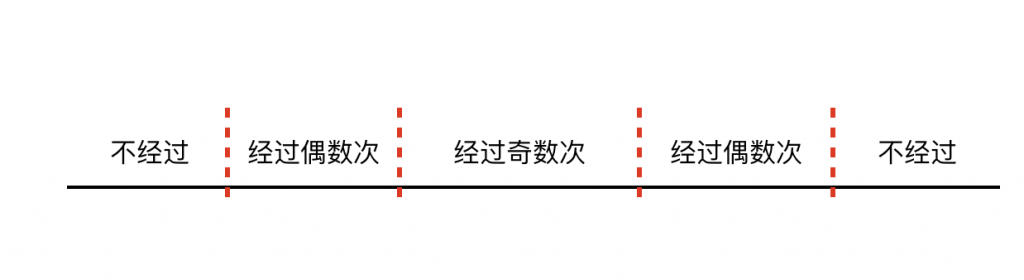 无论 Snuke 怎么走都会符合这个模型,只是可能有一些部分不会出现。如果发现了这个,后面只要直接 DP 就可以了。设 $f[i][j]$ 为第 $i$ 个位置属于第 $j$ 个部分的代价,转移时加上每个部分相应的代价即可。
无论 Snuke 怎么走都会符合这个模型,只是可能有一些部分不会出现。如果发现了这个,后面只要直接 DP 就可以了。设 $f[i][j]$ 为第 $i$ 个位置属于第 $j$ 个部分的代价,转移时加上每个部分相应的代价即可。