Dylan's Blog

比赛链接：http://acm.hdu.edu.cn/contests/contest_show.php?cid=909

B - Graph Theory Class

令 $f(n)$ 为小于等于 $n$ 的质数个数，答案其实就是

$$\sum_{i=3}^{n+1}i+f(n+1)-1$$

然后用 min_25 求 $f(n)$ 即可

代码链接

E - Lunch

设只有一根长度为 $l_i$ 的巧克力局面的 SG 值为 $SG(l_i)$

那么当前局面 SG 值就为 $\bigoplus_{i=1}^{n} SG(l_i)$

令 $pri$ 为任意不为 $2$ 的质数，那么 $SG(x\cdot pri)=SG(pri)+1$。当 $x$ 为奇数时，类似的有 $SG(x\cdot 2)=SG(x)+1$；当 $x$ 为偶数时，考虑 $x$ 获得 $SG(x)$ 级胜态的策略，$1$ 级胜态的局面为奇数根长度为 $2$ 的巧克力，如果 $SG(x*2)$ 采取相同的策略，最后的局面则为奇数根长度为 $4$ 的巧克力，此时 SG 值仍然为 $1$。因此 $x\cdot 2$ 不存在获得 $SG(x)+1$ 级胜态的策略，即此时 $SG(x\cdot 2)=SG(x)$。

代码链接

F - Robotic Class

考虑每个区间的临界点，将其分别放入左右区间的路径上去模拟，如果到达 $n$ 点的数值不同，则函数不连续。

模拟其实用 DFS 和 BFS 均可，下面代码是我用 BFS 的写法。

代码链接

M - Residual Polynomial

对分治 FFT 的理解还不够到位，比赛时没有想出来。

先考虑 $ai$ 对 $w{i-j}$ 的贡献。感性理解一下， $f{1}$ 经过了 $j$ 次求导和 $n-j$ 次平移后，$a_i$ 的贡献才能加在 $w{i-j}$ 上。因此我们令 $dj$ 为 $\prod{i=2}^{n}(bix+c_i)$ 的第 $j$ 项系数，那么 $a_i$ 对 $w{i-j}$ 的贡献就为 $a_i\cdot d_j\cdot i!/(i-j)!$ 。

令 $ai\cdot i!$ 的母函数为 $f(x)$，$d{n-i}$ 的母函数为 $g(x)$，那么 $f(x)\cdot g(x)$ 就是 $w_{i+n}\cdot i!$ 的母函数。

代码链接

3 月 23 日 AtCoder Grand Contest 032 比赛链接：https://atcoder.jp/contests/agc032

B - Balanced Neighbors

思路： 当 $n$ 为偶数时，可以把点 $(i,n-i+1)$ 配对，然后每个点向与它一对之外的所有点连边；当 $n$ 为奇数时，把点 $(i,n-i)$ 配对，同样每一点向与它一对之外的所有点连边（包括 $n$ ）。

代码链接

C - Three Circuits

思路：

因为是连通图，你可以把三个环拼成一条欧拉回路，因此如果这张图含有奇度数的点，则一定不存在构造方案。如果有一个点的度数大于等于 $6$，代表着这条欧拉回路经过了这个点至少 $3$ 次，而每一次都可以形成一个环，所以这样是一定存在构造方案的。

经过上面讨论后，剩下的图只有度数为 $4$ 和度数为 $2$ 的点。如果一张图度数为 $4$ 的点大于等于 $3$ 个，那么所有构成环的情况分为下面两种: 存在一条路径从一个度数为 $4$ 的点出发，不经过其他度数为 $4$ 的点并且回到出发点；一条路径经过两个度数为 $4$ 的点一次，并形成了环。可以发现这样的图至少存在 $3$ 个环。

剩下的情况中如果度数为 $4$ 的点少于两个，那么显然是不存在构造方案的。如果度数为 $4$ 的点恰有两个，就只有下图两种情况，只有这张图的最小割为 $2$ 时才存在构造方案。所以可以用一个 BFS，模拟一下最大流的过程判断这张图的割。

代码链接

D - Rotation Sort

思路：

首先转换一下题意，题目中的一次操作可以看成：从序列中取出一个元素，将它插入前面或后面的一个位置，分别花费 $A$ 或 $B$ 的代价。不难发现每一个元素最多会被操作一次，且有些元素不会被操作。我们就可以从这入手设计 DP 状态。设 $f_{i,j}$ 表示处理完前 $i$ 个数且最后一不会被操作的数为 $j$ 所花费的最小代价，然后根据题意简单地转移一下就好。

代码链接

E - Modulo Pairing

思路：

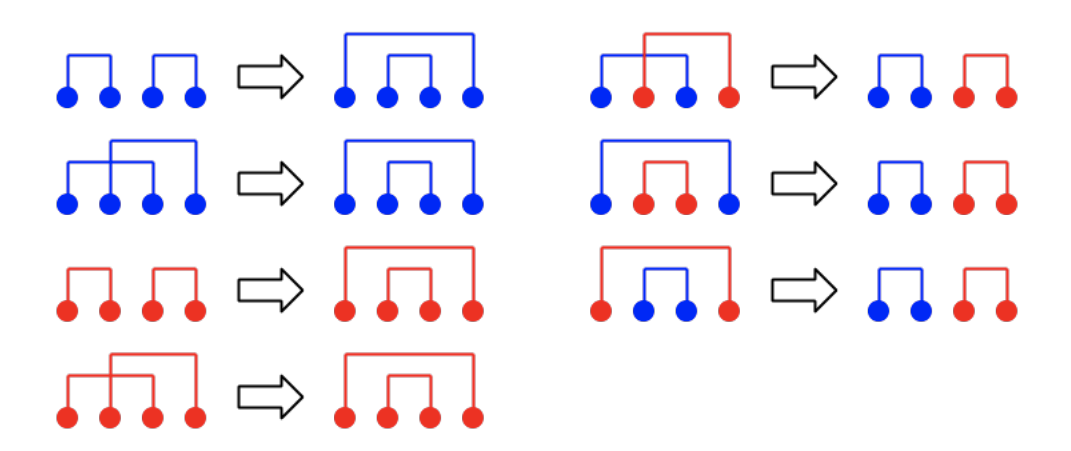
假设 $lim$ 已知，考虑对于数 $x$，我们要找到一个 $y$ 与它配对，使得 $x+y$ 在模 $m$ 意义下不超过 $lim$。 如果 $x+y < m$，那么 $y$ 最大可以取 $lim-x-1$ ;如果 $x+y > m$，那么 $y$ 最大可以取 $lim+m-x$。我们让 $y$ 在对应的取值范围内选尽量大的数一定不会更劣，所以假如对于一个 $x$，我们决定了与它配对的 $y$ 与 $m-x$ 的关系，那么 $y$ 的值我们也可以确定。

考虑这样一个结论：将所有数排好序后，设最大值为 $x{max}$，如果一个数 $x$ 大于 $m-x{max}$，那么与它配对的 $y$ 就一定比 $m-x$ 大; 否则一定比 $m-x$ 小。这样以来我们就可以二分出一个位置 $pos$，在 $pos$ 左边的数两两配对小于 $m$，在 $pos$ 右边的数两两配对不小于 $m$。确定出 $pos$ 后，答案就可以跟着确定下来。

对于结论的正确性，我们可以对所有情况进行讨论。设蓝色的线为小于 $m$ 的匹配，红色的线为不小于 $m$ 的匹配，根据下图可以发现该结论对于所有情况均成立：

代码链接

问题描述

给定一棵 $n$ 个点的有根树，其中 $1$ 号点是根节点。每个节点都被染上了某一种颜色，其中第 $i$ 个节点的颜色为 $c_i$。定义 $dep_i$ 为 $i$ 节点与根节点的距离，为了方便起见，你可以认为树上相邻的两个点之间的距离为 $1$。

站在这棵色彩斑斓的树前面，你将面临 $m$ 个问题。每个问题包含两个整数 $x$ 和 $d$，表示询问 $x$ 子树里且 $dep$ 不超过 $dep_x+d$ 的所有点中出现了多少种本质不同的颜色。

输入

第一行包含一个正整数 $T(1<=T<=500)$，表示测试数据的组数。
每组数据中，第一行包含两个正整数 $n$ 和 $m (1 \leq n,m \leq 100000)$，表示节点数和询问数。
第二行包含 $n$ 个正整数，其中第 $i$ 个数为 $ci (1 \leq c_i \leq n)$，分别表示每个节点的颜色。
第三行包含 $n-1$ 个正整数，其中第 $i$ 个数为 $f{i+1} (1 \leq f_i<i)$，表示节点 $i+1$ 的父亲节点的编号。
接下来 $m$ 行，每行两个整数 $x(1 \leq x \leq n)$ 和 $d(0 \leq d \leq n)$，依次表示每个询问。
输入数据经过了加密，对于每个询问，如果你读入了 $x$ 和 $d$，那么真实的 $x$ 和 $d$ 分别是 $x \oplus last$ 和 $d \oplus last$，其中 $last$ 上一次询问的答案。
输入数据保证 $n$ 和 $m$ 的总和不超过 $500000$。

输出

对于每个询问输出一行一个整数，即答案。

思路

方法一： 如果这个问题在序列上且离线的话，可以发现这就是「HH的项链」。其中一个比较好的思路就是先将询问排序，从左到右扫一遍，我们将每种颜色的贡献算在这种颜色最右边的点上，用树状数组维护区间和即可。强制在线怎么办？可持久化一下，每个右端点都建一个线段树即可。

把这个放在树上也是一样，按深度从大到小考虑，我们将每种颜色的贡献算在这种颜色最浅的点上，用一个以深度为下标的线段树计算子树的答案，然后从下到上线段树合并就好。同时再开一个以颜色为下标的线段树维护深度，同样从下向上合并，合并时把较深的一点贡献在计算答案的线段树上删去。强制在线怎么办？将线段树合并的过程可持久化一下就好。空间复杂度似乎是多一个 $\log n$ 的。

方法二： 类似的从序列上的问题考虑。还有一种想法就是，从左到右扫一遍，每当加入一个颜色的点时，加上这个点的贡献，并删去这个颜色上一个点的贡献，同样用树状数组维护区间和就好。

如果把这个放在树上，就是按深度从小到大考虑，每增加一个颜色的点时，就加上这个点的贡献，并在它和与它颜色相同且相邻的点的 LCA 上删去贡献（这里的相邻是指 dfs 序上两点之间没有其他相同颜色的点）。因为一棵子树的 DFS 是连续一段，这样就可以按深度从小到大扫，用线段树维护子树区间和即可。强制在线怎么办？可持久化，每个深度都建一个线段树就好。

代码

嘴巴选手，懒，不想写代码

第一类斯特林数

定义：

表示 $n$ 个不同元素形成 $m$ 个圆排列的方案数，记为 $\begin{bmatrix} n \ m \end{bmatrix}$。

性质：

首先考虑这个怎么求，可以枚举第 $n$ 个元素，它可以自己形成一个新的环，方案数为 $\begin{bmatrix} n-1 \ m-1 \end{bmatrix}$；它也可以放在已有的 $n-1$ 个元素中一个的后面，方案数为 $(n-1)\begin{bmatrix} n-1 \ m \end{bmatrix}$，从而得出递推式:

$$\begin{bmatrix} n \\ m \end{bmatrix} = \begin{bmatrix} n-1 \\ m-1 \end{bmatrix} + (n-1)\begin{bmatrix} n-1 \\ m \end{bmatrix}$$

我们设 $f_n(x)$ 为 $\begin{bmatrix} n \ x \end{bmatrix}$ 的生成函数。根据上面式子可以写出它的生成函数

$$f_n(x)=\prod_{i=0}^{n-1} (x+i)$$

而这个可以直接套用分治 FFT 在 $O ( n \log^2 n )$ 内求出，但我们还可以在它的基础上优化。考虑你目前分治到区间 $(l,r)$，在这之前已经计算出了区间 $(l, mid)$ 的卷积，这个时候应该要递归的计算 $(mid+1, r)$ 的卷积，但其实发现如果你设 $(l, mid)$ 的卷积为 $g(x)$，那么 $(mid+1,r)$ 的卷积就是 $g(x+mid)$。将式子如下化简：

$$\begin{aligned} g(x+mid)=&\sum_{i=0}^{n} a_i(x+mid)^i\\ =&\sum_{i=0}^{n} a_i\sum_{j=0}^i {i\choose j}mid^{i-j}x^j\\ =&\sum_{i=0}^{n} x^i \sum_{j=i}^{n}{i\choose j}mid^{j-i}a_j\\ =&\sum_{i=0}^{n} \frac{x^i}{i!} \sum_{j=i}^{n}\frac{mid^{j-i}}{(j-i)!}a_j\cdot j! \end{aligned}$$

你发现后面的那一块有点像卷积的形式，将其中一项反转后就可以卷起来了，这样我们做到 $O(n \log n)$ 的复杂度

3 月 8 日 Codeforces Round #545 比赛链接：https://codeforces.com/contest/1138

E - Museums Tour

思路：

首先考虑将每一个 museum 按天数分为 $d$ 个点，然后对应的向相邻的连边。接着就很自然的想到用 tarjan 缩点，然后考虑如何统计答案。有一个性质就是如果一个 museum 对应不同天的点之间有边，那么这些点一定是在同一个强联通分量里面的，因此你缩点后直接找一个包含 museum 数最多的链就是对的。

代码链接

F - Cooperative Game

思路： 如果你知道 pollard-rho 中的 floyd 判环的话，这题的思路就应该不难想到。如果你直接模拟这个过程：让一个人每次走一步另一个人每次走两步，就能够在 $2*(t+c)$ 次交互内让两个人在环上相遇。那么问题就在于如何不知道终点位置的情况下让所有人走到终点。这里有个非常巧妙的性质就是在相遇点走 $t$ 步后一定能到达终点，如果我们设两个人分别走了 $t+x$，$2t+2x$ 步后相遇，那么 $t+x$ 一定是环长的倍数，如果再走 $t$ 步就意味着在环上总共走了 $t+x$ 步（一开始在链上走了 $t$ 步），那么就一定走到了终点。因此只要让一些人留在起点，两个人在环上相遇后所有一起走若干步，如果大家全部相遇，就意味着已经到终点了。

代码链接