Dylan's Blog
0%

Posted on Edited on In

这次济南区域赛还是是踩线拿的银奖，开了两道银牌题都没有写出来。平时训练效率确实有些低，训练时不够专注。以后需要改进：

  1. 进行模拟赛时要写满五个小时，严格按照正式比赛流程进行
  2. 以周为单位，系统地对竞赛知识点进行复习
  3. 在 Codeforces, Atocer 网站上补题时，以重现赛的方式进行

这次比赛时，和队友都交流配合更加默契了。比赛过程中还是要注意以下两点：

  1. 与队友交换想法时一定要有明确的思路，把细节想清后再讨论
  2. 讨论一题时双方都应该对题目有一定的思考，防止队友被误导

Posted on Edited on

CSUAutoselect

中南大学自动选课工具 V1.3

作者：@DavidHuang

安装

Python3

该项目需要 Python3，可以从 Python 官网 下载并安装

Repo

点击右上角的 Clone or download 下载该项目至本地

对于 git 命令行：

1
$ git clone https://github.com/CrazyDaveHDY/CSUAutoSelect.git

requests模块

在命令行中运行：

1
$ pip3 install requests

运行

进入项目根目录，命令行中运行

1
$ python3 autoselect.py

按照提示输入学号，教务系统密码，课程 ID 后即可开始自动选课

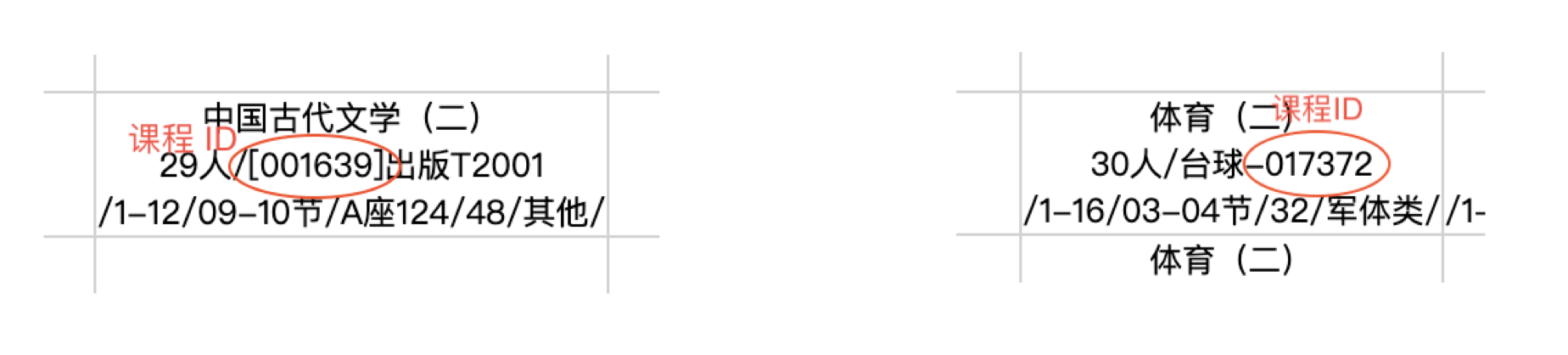
课程 ID 查找方法：在 中南大学教务系统课表查询页面 中点击「按教师」按钮，输入学年学期、教师名称后点击「查询」，格子中央的 6 位数字编号即为课程 ID。

课程 ID.png

许可协议

CSUAutoSelect GPL-3.0 License

Posted on Edited on In

上海站这次队伍好多啊，踩线拿到了 AG，以下是一些总结：

  1. 签到写的慢，还 WA 了很多发，前两小时才写完签到。以后要多打打 CF 的比赛，不能是光写题。
  2. D 题我一开始讨论方向错了，写了一个小时仍然无法处理一些细节情况，这一小时完全浪费了，队友也没能写代码。以后写一份很花时间的代码之前要先充分和队友讨论，明确思路。
  3. 前期浪费的时间有些多，最后 C 的数位 DP 没有调出来，有一点遗憾。全队一直受到 D 题的影响，漏掉了 H 没有做出来。还是要分配好任务，最后时应该要有人专攻 H 题，H 可能就不会被漏掉。

Posted on Edited on In

比赛链接：https://vjudge.net/contest/404866

B - Chessboard

首先可以发现最后一个上色的块一定在四个角上。接着考虑倒着推，根据题目的要求发现每次必须把一行或者一列上的色块全部上满色。把操作顺序反过来后，如果给某一行上色时留下一部分不上色，那么后续将这一部分补上颜色时一定会与题意矛盾。

考虑从四个角的任意一个开始，有 $n-1$ 行 $m-1$ 列需要上色，每次上色可以在行和列中选一个上色，因此有 $4 \cdot {n+m-2 \choose n-1}$ 种方案

行数或列数为 $1$ 的情况需要特判。

代码链接

H - Prince and Princess

不难发现，如果说真话的人数超过一半，则一定可以找到公主的位置，否则有可能无法确定公主的位置。

要特判只有一间房子的情况，比赛时忘了特判卡了很久。

代码链接

I - Space Station

考虑记忆化搜索，搜索的情况数的上限是 $50$ 以内的无序拆分数之和。

当目前的能量值大于 $50$ 时可以直接剪枝，然后还是 TLE。考虑能量为 $0$ 的星球可以任意时候到达且不影响当前能量，搜索时也可以剪枝。

代码链接

J - Spy

比赛时发现这题可以转化为求二分图的最大权完美匹配，遂复制粘贴一波费用流板子，然后 TLE。然后想到了没有学过的 KM 算法，在网上找了几个 KM 板子复制粘贴一波，然后还是 TLE。打算以后真正学 KM 算法的时候再把这题补完。

Posted on Edited on In

比赛链接：http://acm.hdu.edu.cn/contests/contest_show.php?cid=909

B - Graph Theory Class

令 $f(n)$ 为小于等于 $n$ 的质数个数，答案其实就是

然后用 min_25 求 $f(n)$ 即可

代码链接

E - Lunch

设只有一根长度为 $l_i$ 的巧克力局面的 SG 值为 $SG(l_i)$

那么当前局面 SG 值就为 $\bigoplus_{i=1}^{n} SG(l_i)$

令 $pri$ 为任意不为 $2$ 的质数，那么 $SG(x\cdot pri)=SG(pri)+1$。当 $x$ 为奇数时，类似的有 $SG(x\cdot 2)=SG(x)+1$；当 $x$ 为偶数时，考虑 $x$ 获得 $SG(x)$ 级胜态的策略，$1$ 级胜态的局面为奇数根长度为 $2$ 的巧克力，如果 $SG(x*2)$ 采取相同的策略，最后的局面则为奇数根长度为 $4$ 的巧克力，此时 SG 值仍然为 $1$。因此 $x\cdot 2$ 不存在获得 $SG(x)+1$ 级胜态的策略，即此时 $SG(x\cdot 2)=SG(x)$。

代码链接

F - Robotic Class

考虑每个区间的临界点，将其分别放入左右区间的路径上去模拟，如果到达 $n$ 点的数值不同，则函数不连续。

模拟其实用 DFS 和 BFS 均可，下面代码是我用 BFS 的写法。

代码链接

M - Residual Polynomial

对分治 FFT 的理解还不够到位，比赛时没有想出来。

先考虑 $ai$ 对 $w{i-j}$ 的贡献。感性理解一下， $f{1}$ 经过了 $j$ 次求导和 $n-j$ 次平移后，$a_i$ 的贡献才能加在 $w{i-j}$ 上。因此我们令 $dj$ 为 $\prod{i=2}^{n}(bix+c_i)$ 的第 $j$ 项系数，那么 $a_i$ 对 $w{i-j}$ 的贡献就为 $a_i\cdot d_j\cdot i!/(i-j)!$ 。

令 $ai\cdot i!$ 的母函数为 $f(x)$，$d{n-i}$ 的母函数为 $g(x)$，那么 $f(x)\cdot g(x)$ 就是 $w_{i+n}\cdot i!$ 的母函数。

代码链接